Riddle Me This, Sommelier

Imagine this: you’re a king or queen. Congratulations! You spend your days doing the normal royal things: laughing at peasants, having lavish feasts, and (most importantly for your job security) thwarting assassination attempts. One of these assassins was pesky though, and managed to poison one of your wine bottles before the guards got him. Even worse - the guards helpfully put the bottle back on the shelf and now can’t remember which one of your 100 bottles is poisoned! This is extra unfortunate because one of your lavish feasts is coming up and you need to use all the wine to effectively mock the peasants.

Your court chemist is clever and comes up with a reagent that will react to the poison. Put a drop of it in a liquid with the poison and it will start to foam, no matter how small a trace of poison there is, meaning you can test just a drop of wine to test if the bottle is poisoned. Unfortunately, you only have enough reagent for running 7 tests. How can you find the poisoned bottle?

This Sounds Familiar…

The above riddle is a famous one that’s been copied around the internet in one form or another, like on the Math Stack Exchange. The key idea is one of the subtleties in the phrasing: I mentioned that the test works no matter how diluted the poison is, which implies you can test multiple bottles of wine at once by mixing together drops of each then testing the mixture. Now that you know you can do that, can you spot a solution?

The solution is to test half the bottles at a time. After you get the results, you know half the bottles are poison free – the ones you tested if it comes back positive, or the ones you didn’t on a negative. Each test halves the results, and after 7 halvings you make it to the one poisoned bottle.

A more difficult version of this riddle requires you run all the tests at the same time. You can still do this with just 7 tests. I’ll leave the puzzling for the riddle-obsessed readers. The ideas in this article might help you solve it. Hint in the footnote.^[1]

This process of testing multiple bottles at once is known as group testing, and it has more practical purposes than solving riddles.

Sharing is Caring, Even in Pandemics

How many Covid tests do you need to test 100 people for Covid? Covid tests can act like our wine poison test, where we can combine the samples of a group of people and test the combination. If the test comes back negative, then it is highly likely that everyone in the group is negative. Otherwise, more tests can be run to determine who in the group was “responsible” for the positive result.

Don’t worry, we aren’t sharing cotton swabs! We combine the samples afterwards like responsible tyrannical monarchs scientists.

Here’s an example. I’ve designed a 3-stage testing procedure as follows:

Stage 1: Split people into groups of 6 and test each group.

Stage 2: Put everyone who tested positive in stage 1 into new groups of 3 such that no two people were in the same group in stage 1 and test each new group.

Stage 3: Using one test per person, test everyone who was in a group that tested positive in stage 2.

Result: Everyone who got a positive test in stage 3 has Covid, everyone else does not.

Since we can’t rely on people coming back to the lab twice for follow up tests, we need to gather enough of a sample from everyone to perform 3 tests. This probably entails swabbing everyone multiple times but that sometimes depends on the test.

Unlike the wine problem, we don’t know how many people are positive in our testing population. However, most countries gather enough data to know the probability someone will get a positive test, including the United States. As of writing, about 10% of tests we run on individuals in the US come up positive, a value called the test positivity rate (this doesn’t include at home tests, but we can’t do home testing in groups anyways). Since this is probabilistic, we can’t guarantee we will save tests. Instead, we need to see if we can reduce the average number of tests used.

You could nerd out and compute the average for the example yourself, or you could just trust me when I say that with a 10% positivity rate there’s a 47% chance of a positive in stage 1 and 51% for stage 2, meaning only 24% of participants move to stage 3 and get individual tests. By these results, I did more math to find that we only use an average of 56 tests per 100 people, or 0.56 tests per person.

Those are Rookie Numbers

Can we do better? There is a theoretical minimum on the number of tests we will need to perform on average. This minimum can be found using information theory, a math framework for measuring how efficiently data can be communicated. At first glance, it does not seem like this problem has anything to do with communication. To a mathematician, however, communication is merely sending and receiving data to teach or learn something. In this case, we want to learn whether each person does or does not have Covid, and we are being given data in the form of Covid test results. So, at least mathematically, we can model our problem as trying to communicate who has Covid through the test results.

The basic unit of information theory is the bit, which measures the maximum amount of information that can be learned by receiving the answer to a single yes-or-no question. Each Covid test has only two results, which means we can learn everything we need about it with a single question: “is this test positive?” Therefore, each test provides no more than one bit of information.

The information we want to learn is whether someone has Covid. Information theory has a function called the binary entropy function that tells us the average number of bits it takes to communicate the outcome of a probabilistic event with two possible outcomes. Since someone has Covid 10% of the time, we plug in 10% to this formula to find that we require an average of 0.47 bits per person to communicate their Covid status. It is impossible to beat this threshold. This implies we cannot do better than 47 tests per 100 people on average. Considering our previous plan is at 56, we are doing pretty good! With a lower test positivity rate, we could do even better.

In practice, we cannot actually reach the information-theoretic lower bound. For example, at a test positivity rate of 38% it is mathematically impossible to beat testing people individually despite the information theoretic bound being 96 tests per 100 people. This is because the bound is only reached when each Covid test is providing a full bit of information, which by the binary entropy function requires each test has a 50% chance of being positive. Each test will almost certainly have a probability slightly above or below 50%, making the bound impossible. Nevertheless, a good rule of thumb for an efficient test is to make the probability of it being positive as close to 50% as possible, which is how I designed the 3-stage example.^[2]

There are other factors that make this efficiency more difficult in practice. The underlying test has false positive and negative rates and pooling samples can cause this error to increase. Mathematicians have models that take this into account, though it does make it more complicated. Fortunately, we can use extra tests as error correction to make up for the increased error from pooled tests and still be better than the 1 test per person solution in many cases.

Testing for the Impatient

The example I used is called an adaptive method, because who we test next depends on the results of the previous tests. While this is the most optimal for reducing the number of tests performed, it is going to substantially slow down how long it takes to get test results since we will often need to wait for one round of tests to complete before starting the next one. When it comes to quarantining Covid patients, speed is important. On the other hand, non-adaptive tests run all the tests at the same time, getting results much faster.

Non-adaptive tests can be difficult to design. Luckily, dice are smarter than we are. The non-adaptive method Wikipedia discusses on the group testing page is called COMP, and it just creates all the test groups at random yet has some very nice properties. There are more sophisticated testing setups that can beat rolling dice, like one that exploits the properties of prime numbers or other fancy math.

There is a big catch to non-adaptive methods. With an adaptive method, we usually use the final round of testing to test individuals for whom we still have inconclusive results – people who have only been in groups with positive tests but could still potentially be negative, like those who got a positive result in stage 2 of our example. The only way to guarantee removing inconclusive results is to run individual tests. With non-adaptive methods, we can’t do this because we won’t know which individuals have inconclusive results until after testing is finished. This means there is always a chance someone gets an inconclusive instead of a straight positive or negative. Well-designed non-adaptive methods can guarantee this won’t happen as long as the number of people in the test with Covid is below a certain threshold, like how in our wine problem we can guarantee no inconclusives if there is only 1 poisoned bottle, even if we run all the tests at the same time. But if you test a group with an unusually large number of positive cases, then you are out of luck.

Here’s an example – say we are testing 36 people at a time. Put them in a 6x6 table and perform a group test on every row, every column, and every diagonal with diagonals wrapping around from bottom to top and right to left. The picture below shows an example. All three groups that person 14 is in are shaded in, each group in a different color, where the diagonal group in gray wraps around from the bottom of the table to the top to include person 6.

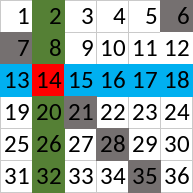
This method puts each person in three groups, giving us 0.5 tests per person. Already we know this is a bad setup – we need to be using more tests than the adaptive version to deal with inconclusives, and we have less. The results bare this intuition out.

If 2 or fewer people have Covid, they will be identified as the only people with no negative tests and there will be no inconclusive results. But if 3 or more people are positive, then any person who shares a row, column, and diagonal with someone who is positive will have inconclusive results.^[3] In our example, if person 7, 16, and 32 were positive then 14 would be inconclusive. With our 10% test positivity rate, 11% of people would get inconclusive results. In fact, with as few as 6 positive cases in the batch it is possible for everyone’s result to be inconclusive, effectively wasting all the tests. We can soften this by placing everyone in a fourth group, adding 6 more tests.^[4] Then, we could reduce the probability of an inconclusive to 6%.^[5] More sophisticated methods can yield much better results.

Inconclusive results are unfortunate. Some of you might think this possibility is so bad that this shouldn’t be done. As a compromise, having two stages lets us remove all inconclusive results. This tends to get the best of both worlds. Only those who tested inconclusive in the first stage need to wait longer for their results – most people will see no slowdown. And if the inconclusive rate is low, this won’t use many more tests.

One of the first papers on group testing only considered very simple two-stage tests. Specifically, it looked at setups where participants were tested in a single group and (if necessary) a follow-up individual test. It concluded that for our positivity rate the optimal group size is 4, leading to an average of 0.59 tests per person.

Is This Worth the Complications?

These aren’t huge savings. We managed to cut the tests used roughly in half, but with a lower test positivity rate we could easily get much better. For a positivity rate of 3%, we could get to 0.34 tests per person in a simple two-stage test. The high test positivity rate is due to the fact that most of the people who choose to get tested are already feeling sick, and those using the fancier tests in doctors offices and hospitals (where we could plausible group test) are often even sicker. With lower positivity rates we could get huge savings, making them great for tasks where we are looking for asymptomatic carriers and expect most people to come back negative. Examples include testing all students when the school year starts or testing all inbound immigrants before they enter the country. Lowering the cost of testing means we can test more people and test people more often, which is the best way to keep the virus quarantined while letting most people go about their ordinary lives.

There was some real world usage of these techniques. I found articles discussing how Rwanda, Israel and Nebraska used group testing, and I am sure there are more. In addition, there are designs for non-adaptive tests that you can download yourself and some very smart people researched some fancy techniques for Covid tests and built an app to help lab techs run these in the field.

However, from my dive in the topic, it seems that most of the research is from the theoretical math side, with only limited interest from biologists. The Nebraska article discussed how they needed special permission from the Governor to run group testing because the test manufacturers didn’t build the tests for multiple people and wouldn’t guarantee it would work. While they did have evidence that the tests remained effective in groups, more research is needed so we can intentionally build tests designed for this kind of thing in the future.

Cost now might not be a huge deal, considering Covid tests are now in relatively large supply. However, I think we should be planning ahead for the next potential pandemic. Early on we would expect that, like Covid, tests would be in short supply but testing would be critical to stemming the spread. Being able to use these tests efficiently could make a huge difference in this scenario. However, something like this requires practice and research, and right now when we are still doing testing in bulk is the perfect time to do so. We should be experimenting with group testing now so we are prepared to use it in the future. Though you might have to get an extra cotton swab up your nose to do it.

Now shoo peasant, there’s a bottle of wine with my name on it.

---

Footnotes

1. HINT: it might be helpful to write the bottle numbers in binary. ↩︎

2. This isn’t to say that this produces the best possible outcome. Sometimes having one test farther away from 50% now enables you to have more tests closer to 50% later. Just picking the test with the closest probability to 50% each time is what is known as a greedy algorithm, which produces pretty good results quite easily at the expense of missing the optimal solution. ↩︎

3. We still can learn about people with inconclusive results though. On average, the probability someone with an inconclusive has Covid is 45% (with 4 groups, 47%), far higher than our baseline 10%. We can get a more precise number when looking at the actual test results. The reason we learn something is because there are often multiple inconclusives in the same group with no definitive positive case. This implies one of the inconclusives must be positive, raising the probability any one of them is positive. ↩︎

4. Unfortunately, there will be some overlap between testing groups ↩︎

5. The probability for being inconclusive is difficult to calculate. It is easy to calculate if we assume the person with the inconclusive is negative, but if they are positive we need to calculate the probability that other people in their groups get either a positive or an inconclusive which becomes a mess due to the recursion and the interdependence of the testing groups. Instead, I wrote a Python script to simulate the test 100,000 times to get these numbers. ↩︎